|
• sinθ+cosθ, sinθcosθの値 • 三角方程式(2次) • 三角不等式(2次) ♫♣ 元の教材が通信トラブルなどで読めないときに,こちらを使ってください.なお,学習の記録は付いていません. |
|
■三角比の相互関係 《解説》
○ 高校数学Iで登場する「三角比の相互関係」とは,次の2つの公式のことです.
三角比sinA , cosA , tanAのうち1つ分かれば,残りはこれらの公式を使って「芋づる式に」求まります. ○ 例えば,sinAが分かれば(1)を使ってcosAが求まり,さらに(2)を使ってtanAが求まります. しかし,例えばtanA = のように,三角比のうちでtanAだけが与えられて残りのsinA , cosAを求めるときは要注意です. (2)からsinA=3 , cosA=4などと間違う生徒が多いからです.(−1≦sinA , cosA≦1を満たしていないので,間違いに気づくはずです.比だけが与えられているのだから,3/2:4/2 あるいは3/5:4/5などの可能性も考えなければなりません.) このように,tanA ⇒ cosA(またはsinA)の関係式が必要なときは,(1)の両辺をcos2A(またはsin2A)で割って次の公式(3)(4)を「その場で作ればよい」.(「公式」を覚えるのでなく,必要になったときに作るようにします・・・「公式がある」ということだけを覚えておく…覚えなければならない公式の数を減らして,公式間の関連をつかむようにする)
tan2A+1 =
1+ |
例1
sinA = (0°≦A≦180°)のときcosAの値を求めてください.
(答案)sin2A+cos2A=1にsinA = を代入すると ( )2+cos2A=1 cos2A=1−= cosA= 右図のようにsinA = のとき,Aは第1象限の場合も第2象限の場合もあり,これに対応するcosAの値は,第1象限なら正,第2象限なら負の値になる.(どちらも可能) ゆえに,cosA= |
|
例2
cosA = (0°≦A≦180°)のときtanAの値を求めてください.
(答案)sin2A+cos2A=1にcosA = を代入すると sin2A+( )2=1 sin2A=1−= sinA=± 右図のようにcosA = のとき,Aは第1象限の角で,これに対応するsinAの値は正の数になる. ゆえに,sinA= このとき,tanA= =
(別解)
この答案では公式(1)を使ってcosA → sinA 公式(2)を使ってsinA , cosA → tanA のように2段階で求めたが,公式(3)を使って,cosA → tanAのように直接求めることもできる. |
例3
tanA = − (0°≦A≦180°)のときcosAの値を求めてください.
■注意■
(答案)tanA = だからといって cosA = − 2 , sinA = 比率が− になるものには, 組合せがあります. 実際には,これらのうちでsin2A+cos2A=1を満たすものだけが答になりますが,その値は公式(3)で求まります. 公式(1)の両辺をcos2Aで割って,公式(3)を作る. tan2A+1 = …(3) (3)にtanA = − を代入すると (− )2+1= = cosA=± 右図のようにtanA = − のとき,Aは第2象限の角で,これに対応するcosAの値は負の数になる. ゆえに,cosA= − …(答) |
|
【問題1】 選択肢の中から正しいものをクリックしてください
選択肢をクリックすれば,採点結果と解説が出ます.見ているだけでは,解説は出ません
(1)
sinA = (0°≦A≦180°)のときcosAの値を求めてください.
sin2A+cos2A=1にsinA = を代入すると
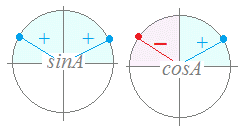 ( )2+cos2A=1
cos2A=1−=
cosA=±
( )2+cos2A=1
cos2A=1−=
cosA=±sinA = のとき,Aは第1象限または第2象限の角で,これに対応するcosAの値は正負どちらもある. ゆえに,cosA= ±…(答) |
(2)
sinA= (0°≦A≦180°)のときcosAの値を求めてください.
sin2A+cos2A=1にsinA = を代入すると
 ( )2+cos2A=1
cos2A=1− =
cosA=± ( )2+cos2A=1
cos2A=1− =
cosA=±sinA = のとき,Aは第1象限または第2象限の角で,これに対応するcosAの値は正負どちらもある. ゆえに,cosA= ±…(答) |
|
(3)
cosA= (0°≦A≦180°)のときsinAの値を求めてください.
sin2A+cos2A=1にcosA = を代入すると
 sin2A+( )2=1
sin2A=1− =
sinA=±
sin2A+( )2=1
sin2A=1− =
sinA=±cosA = のとき,Aは第1象限の角で,これに対応するsinAの値は正. ゆえに,sinA= …(答) |
(4)
cosA=− (0°≦A≦180°)のときsinAの値を求めてください.
sin2A+cos2A=1にcosA = − を代入すると
 sin2A+(− )2=1
sin2A=1− =
sinA=± sin2A+(− )2=1
sin2A=1− =
sinA=±cosA = − のとき,Aは第2象限の角で,これに対応するsinAの値は正. ゆえに,sinA= …(答) |
|
(5)
cosA=− (0°≦A≦180°)のときtanAの値を求めてください.
sin2A+cos2A=1にcosA = − を代入すると
 sin2A+(− )2=1
sin2A=1− =
sinA=± sin2A+(− )2=1
sin2A=1− =
sinA=±cosA = − のとき,Aは第2象限の角で,これに対応するsinAの値は正. ゆえに,sinA= このとき,tanA= = − …(答) (別解) 公式(3) tan2A+1= にcosA = − を代入すると tan2A+1= tan2A= tanA= ± cosA = − のとき,Aは第2象限の角で,これに対応するtanAの値は負. tanA= − …(答) |
(6)
sinA= (0°≦A≦180°)のときtanAの値を求めてください.
sin2A+cos2A=1にsinA = を代入すると
 ( )2+cos2A=1
cos2A=1− =
cosA=± ( )2+cos2A=1
cos2A=1− =
cosA=±sinA = のとき,Aは第1象限または第2象限の角で,これに対応するcosAの値は正負どちらもある. ゆえに,cosA= ± このとき,tanA= = ± …(答) (別解) 公式(4) 1+ = にsinA = を代入すると 1+ = tan2A= tanA= ± sinA = のとき,Aは第1象限または第2象限の角で,これに対応するtanAの値は正負どちらもある. tanA= ± …(答) |
|
(7)
tanA= (0°≦A≦180°)のときcosAの値を求めてください.
公式(3) tan2A+1= にtanA = を代入すると
()2+1= cos2A= cosA= ± tanA = のとき,Aは第1象限の角で,これに対応するcosAの値は正. cosA= …(答) |
(8)
tanA=− (0°≦A≦180°)のときsinAの値を求めてください.
公式(4) 1+ = にtanA = − を代入すると
1+(− )2= sin2A= sinA= ± tanA = − のとき,Aは第2象限の角で,これに対応するsinAの値は正. sinA= …(答) |
|
【問題2】 次の式に等しいものを下の選択肢の中から選んでクリックしてください
選択肢をクリックすれば,採点結果と解説が出ます.見ているだけでは,解説は出ません
(1)
(sinA+cosA)2 |
(2)
(sinA−cosA)2 |
|
(3)
|
(4)
|
|
(5)
|
(6)
|
|
(7)
|
(8)
|
|
(9)
|
(10)
|
|
【問題3】 次の式に等しいものを下の選択肢の中から選んでクリックしてください
選択肢をクリックすれば,採点結果と解説が出ます.見ているだけでは,解説は出ません
(1)
|
(2)
|
|
(3)
|
(4)
|
|
(5)
|
(6)
|
|
(7)
|
(8)
|
|
(9)
|
(10)
|





コメント